Floyd-Warshall Algorithm: A Python Guide

The Floyd-Warshall algorithm is a classic algorithm used to find the shortest paths between all pairs of nodes in a weighted graph. It is particularly useful for solving problems where you need to determine the shortest paths between every pair of nodes in a graph, such as in network routing or urban planning. This blog will walk you through the Floyd-Warshall algorithm, its implementation in Python, and some practical examples.

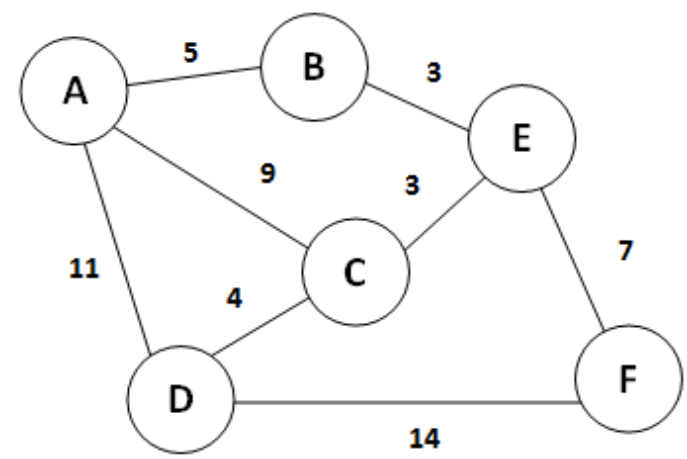
Overview of the Floyd-Warshall Algorithm

The Floyd-Warshall algorithm is an example of dynamic programming. It works by iteratively improving the solution to the shortest path problem using a series of relaxations. The algorithm maintains a matrix of shortest path estimates and updates it based on the shortest paths discovered during each iteration. The core idea is to check if the shortest path between two nodes can be improved by passing through an intermediate node.

Key Concepts of the Floyd-Warshall Algorithm

• Distance Matrix: A 2D matrix where the entry at [i][j] represents the shortest distance from node i to node j.

• Intermediate Node: A node that can potentially be used as a stepping stone to find shorter paths between two other nodes.

Algorithm Steps

1. Initialization: Create a distance matrix where the distance between each pair of nodes is initialized based on direct edges. If there is no direct edge, set the distance to infinity.

2. Relaxation: For each node, update the distance matrix by considering if passing through the current node provides a shorter path between every pair of nodes.

3. Final Matrix: After all iterations, the distance matrix contains the shortest paths between all pairs of nodes.

   
   

Python Implementation for Floyd-Warshall Algorithm

Let’s implement the Floyd-Warshall algorithm in Python. We’ll start by initializing the distance matrix, then perform the relaxation steps, and finally print the shortest paths.

import numpy as np

def floyd_warshall(graph):

     # Number of vertices

     num_vertices = len(graph)

     # Initialize the distance matrix

     distance = np.full((num_vertices, num_vertices), np.inf)

     # Distance from a node to itself is zero

     for i in range(num_vertices):

         distance[i][i] = 0

     # Set initial distances based on the graph edges

     for u in range(num_vertices):

         for v in range(num_vertices):

             if graph[u][v] != 0: # Assuming 0 means no edge

                 distance[u][v] = graph[u][v]

     # Floyd-Warshall algorithm

     for k in range(num_vertices):

         for i in range(num_vertices):

             for j in range(num_vertices):

                 if distance[i][j] > distance[i][k] + distance[k][j]:

                     distance[i][j] = distance[i][k] + distance[k][j]

     return distance

# Example usage

graph = [

     [0, 3, 0, 7],

     [8, 0, 2, 0],

     [5, 0, 0, 1],

     [2, 0, 6, 0]

]

distance_matrix = floyd_warshall(graph)

print("Shortest path matrix:")

print(distance_matrix)

Output for the above code:

Shortest path matrix:
[[0. 3. 5. 6.]
 [5. 0. 2. 3.]
 [3. 6. 0. 1.]
 [2. 5. 6. 0.]]

Explanation

1. Graph Representation: The graph is represented as an adjacency matrix where graph[i][j] holds the weight of the edge from node i to node j. If there is no direct edge, it's set to 0 (or infinity if you prefer).

2. Distance Initialization: The distance matrix is initialized to infinity, and the diagonal is set to zero. This reflects the distance from each node to itself.

3. Relaxation: For each intermediate node k, the algorithm checks if a shorter path exists between every pair of nodes i and j via k. If a shorter path is found, it updates the distance matrix.

4. Output: The final distance matrix contains the shortest paths between all pairs of nodes.

Applications Floyd-Warshall Algorithm

• Network Routing: Finding the shortest paths in communication networks.

• Urban Planning: Calculating the shortest routes between multiple locations.

• Transportation: Optimizing routes in logistics and supply chain management.

Conclusion

The Floyd-Warshall algorithm is a powerful tool for finding the shortest paths between all pairs of nodes in a weighted graph. Its dynamic programming approach ensures that the solution is both comprehensive and efficient for small to medium-sized graphs. With its clear Python implementation, you can easily adapt and extend this algorithm for various applications in network analysis and beyond.