Implementing Breadth-First Search (BFS) in Python

In this blog, we’ll explore BFS in detail, understand its working, and implement it in Python. We’ll also discuss its applications and time complexity.

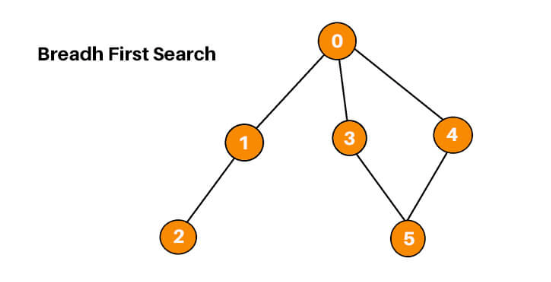
What is Breadth-First Search (BFS) Algorithm?

Breadth-First Search (BFS) is a fundamental algorithm used for traversing or searching tree and graph data structures. BFS starts from a selected node (often called the root) and explores all its neighbors at the present depth before moving on to nodes at the next depth level. This makes BFS particularly useful for finding the shortest path in unweighted graphs and for exploring all nodes in a connected component.

How does Breadth-First Search (BFS) Work?

BFS operates in the following steps:

1. Start at the root node: Select a starting node or root from which the search will begin.

2. Visit all neighbors: Explore all the nodes connected to the current node.

3. Move to the next level: Once all neighbors are visited, move to the next level and repeat the process.

4. Continue until all nodes are visited: The process continues until all reachable nodes are visited.

BFS uses a queue to keep track of nodes that need to be explored. This ensures that nodes are processed in a "first in, first out" (FIFO) manner, ensuring the correct exploration order.

Breadth-First Search (BFS) Implementation in Python

Breadth-First Search (BFS) in Python is a fundamental graph traversal algorithm used to explore nodes and edges of a graph in a systematic manner. It starts from a given source node and explores all its neighboring nodes at the present depth level before moving on to nodes at the next depth level. BFS is particularly useful for finding the shortest path in an unweighted graph. In Python, BFS can be implemented using a queue to maintain the nodes to be explored. The algorithm initializes by enqueuing the starting node and marking it as visited. It then repeatedly dequeues a node, processes it, and enqueues all its unvisited neighbors, marking them as visited as well. This continues until all reachable nodes have been explored. BFS can be applied to both tree and graph structures, making it a versatile tool for problems like pathfinding, network analysis, and solving puzzles like mazes. The simplicity and effectiveness of BFS make it an essential algorithm in the toolkit of any Python programmer. Let’s implement BFS in Python using an example of a simple graph.

from collections import deque

def bfs(graph, start):

     visited = set() # To keep track of visited nodes

     queue = deque([start]) # Initialize the queue with the start node

     while queue:

         vertex = queue.popleft() # Dequeue a vertex from the queue

         if vertex not in visited:

             print(vertex, end=" ") # Process the current node

             visited.add(vertex) # Mark the vertex as visited

             # Enqueue all adjacent nodes that haven't been visited

             for neighbor in graph[vertex]:

                 if neighbor not in visited:

                     queue.append(neighbor)

# Example graph represented as an adjacency list

graph = {

     'A': ['B', 'C'],

     'B': ['D', 'E'],

     'C': ['F'],

     'D': [],

     'E': ['F'],

     'F': []

}

# Perform BFS starting from node 'A'

bfs(graph, 'A')

Output for the code above:

A B C D E F

Explanation of the Code

• Graph Representation: The graph is represented as an adjacency list, where each node is a key in a dictionary, and its neighbors are stored in a list.

• Queue: We use a deque from the collections module to implement the queue. The deque allows for efficient appending and popping of elements.

• Visited Set: This set keeps track of all the nodes that have been visited to prevent cycles and redundant work.

Applications of Breadth-First Search (BFS)

BFS is a versatile algorithm with various applications:

1. Shortest Path in Unweighted Graphs: BFS can find the shortest path from a source to a destination in an unweighted graph because it explores all nodes at the present depth before moving on to nodes at the next depth level.

2. Connected Components: BFS can be used to find all nodes in a connected component of a graph.

3. Level-Order Traversal in Trees: BFS is often used to traverse a tree level by level.

4. Web Crawlers: Web crawlers use BFS to explore the web graph, starting from a set of seed URLs and exploring outward.

5. Social Networking: BFS can be used to find the shortest path or degree of connection between users in a social network.

Time and Space Complexity

• Time Complexity: The time complexity of BFS is O(V+E)O(V+E), where VV is the number of vertices and EEis the number of edges. This is because every vertex and edge is processed once.

• Space Complexity: The space complexity is O(V)O(V) since, in the worst case, all vertices are stored in the queue.

  
  

BFS vs. Depth-First Search (DFS)

While BFS explores all neighbors at the present depth before moving on, Depth-First Search (DFS) explores as far as possible along one branch before backtracking. BFS is better suited for finding the shortest path in an unweighted graph, while DFS is often more memory-efficient and can be more appropriate for problems like topological sorting or solving puzzles.

Conclusion

Breadth-First Search (BFS) is a fundamental algorithm with wide-ranging applications, from pathfinding in unweighted graphs to solving connectivity problems. It’s an essential tool in the arsenal of any computer scientist or software engineer. By understanding and implementing BFS in Python, you’ve taken a significant step toward mastering graph algorithms.

With this foundation, you can now explore more advanced graph algorithms like Dijkstra's or A* search, build on this knowledge to solve complex problems, and implement efficient solutions in your projects.